
SL Paper 1
In a particular week, the number of eggs laid by each hen on a farm was counted. The results are summarized in the following table.

State whether these data are discrete or continuous.
Write down
(i) the number of hens on the farm;
(ii) the modal number of eggs laid.
Calculate
(i) the mean number of eggs laid;
(ii) the standard deviation.
The resting pulse rates of a group of 10 students who exercise regularly are given below.
65, 62, 75, 63, 69, 58, 65, 67, 55, 60
Find the median resting pulse rate of the students.
Find the mean resting pulse rate of the students.
A new student joins the class and the mean resting pulse rate of the group of 11 students becomes 65.
Find the resting pulse rate of the student who joined the group.
The time, in minutes, that students in a school spend on their homework per day is presented in the following box-and-whisker diagram.

Time, in minutes, students spend on their homework per day
Find
(i) the longest amount of time spent on homework per day;
(ii) the interquartile range.
State the statistical term corresponding to the value of 140 minutes.
Find the percentage of students who spend
(i) between 100 and 140 minutes per day on their homework;
(ii) more than 100 minutes per day on their homework.
The grades obtained by a group of 13 students are listed below. \[5{\text{ }}3{\text{ }}6{\text{ }}5{\text{ }}7{\text{ }}3{\text{ }}2{\text{ }}6{\text{ }}4{\text{ }}6{\text{ }}6{\text{ }}6{\text{ }}4\]
Write down the modal grade.
Find the mean grade.
Write down the standard deviation.
Find the interquartile range.
The mean of the ten numbers listed below is 6.8.
8, 5, 5, 10, 8, 4, 9, 7, p, q
Write down an equation in terms of p and q.
The mode of these ten numbers is five and p is less than q.
Write down the value of p.
The mode of these ten numbers is five and p is less than q.
Write down the value of q.
Find the median of the ten numbers.
The distribution of rainfall in a town over 80 days is displayed on the following box-and-whisker diagram.

Write down the median rainfall.
Write down the minimum rainfall.
Find the interquartile range.
Write down the number of days the rainfall will be
(i) between 43 mm and 48 mm;
(ii) between 20 mm and 59 mm.
Eight houses in a street are inhabited by different numbers of people, as shown in the table below.
The following statements refer to the number of inhabitants per house. Write down true (T) or false (F) for each.
The mean is \(5\).
The range is \(4\).
The mode is \(6\).
The standard deviation is \(1.4\) correct to \(2\) significant figures.
Calculate the interquartile range for the number of inhabitants per house.
The cumulative frequency graph represents the speed, s, in \({\text{km }}{{\text{h}}^{ - 1}}\), of 80 cars passing a speed camera.
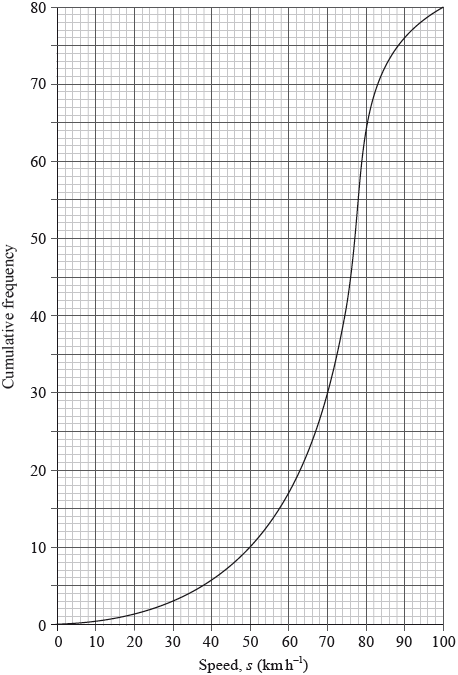
Write down the number of cars passing the camera with speed of less than or equal to 50 \({\text{km}}\,{{\text{h}}^{ - 1}}\).
Complete the following grouped frequency table for \(s\), the speed of the cars passing the camera.

Write down the mid-interval value of the \(50 < s \leqslant 70\) interval.
Use your graphic display calculator to find an estimate of
(i) the mean speed of the cars passing the camera;
(ii) the standard deviation of the speed of the cars passing the camera.
The following six integers are arranged from smallest to largest
1 , x , 3 , y , 14 , z
The mode is 1 , the median is 5 and the mean is 7.
Find x ;
Find y ;
Find z .
For a study, a researcher collected 200 leaves from oak trees. After measuring the lengths of the leaves, in cm, she produced the following cumulative frequency graph.

The researcher finds that 10% of the leaves have a length greater than \(k\) cm.
Write down the median length of these leaves.
Write down the number of leaves with a length less than or equal to 8 cm.
Use the graph to find the value of \(k\).
Before measuring, the researcher estimated \(k\) to be approximately 9.5 cm. Find the percentage error in her estimate.
The following table shows the number of errors per page in a 100 page document.
State whether the data is discrete, continuous or neither.
Find the mean number of errors per page.
Find the median number of errors per page.
Write down the mode.
A survey was conducted of the number of bedrooms in \(208\) randomly chosen houses. The results are shown in the following table.
State whether the data is discrete or continuous.
Write down the mean number of bedrooms per house.
Write down the standard deviation of the number of bedrooms per house.
Find how many houses have a number of bedrooms greater than one standard deviation above the mean.
The weights, in kg, of 60 adolescent females were collected and are summarized in the box and whisker diagram shown below.
Write down the median weight of the females.
Calculate the range.
Estimate the probability that the weight of a randomly chosen female is more than 50 kg.
Use the box and whisker diagram to determine if the mean weight of the females is less than the median weight. Give a reason for your answer.
The daily rainfall for the town of St. Anna is collected over a 20-day period of time. The collected data are represented in the box and whisker plot below.
Write down
(i) the lowest daily rainfall;
(ii) the highest daily rainfall.
State what the value of 12 mm represents on the given diagram.
Find the interquartile range.
Write down the percentage of the data which is less than the upper quartile.
\(240\) cars were tested to see how far they travelled on \(10\) litres of fuel. The graph shows the cumulative frequency distribution of the results.

Find the median distance travelled by the cars.
Calculate the interquartile range of the distance travelled by the cars.
Find the number of cars that travelled more than \(130\) km.
\(80\) matches were played in a football tournament. The following table shows the number of goals scored in all matches.
Find the mean number of goals scored per match.
Find the median number of goals scored per match.
A local newspaper claims that the mean number of goals scored per match is two. Calculate the percentage error in the local newspaper’s claim.
Five pipes labelled, “6 metres in length”, were delivered to a building site. The contractor measured each pipe to check its length (in metres) and recorded the following;
5.96, 5.95, 6.02, 5.95, 5.99.
(i) Find the mean of the contractor’s measurements.
(ii) Calculate the percentage error between the mean and the stated, approximate length of 6 metres.
Calculate \(\sqrt {{{3.87}^5} - {{8.73}^{ - 0.5}}} \), giving your answer
(i) correct to the nearest integer,
(ii) in the form \(a \times 10^k\), where 1 ≤ a < 10, \(k \in {\mathbb{Z}}\) .
Each month the number of days of rain in Cardiff is recorded.
The following data was collected over a period of 10 months.
11 13 8 11 8 7 8 14 x 15
For these data the median number of days of rain per month is 10.
Find the value of x.
Find the standard deviation
Find the interquartile range.
The lengths of trout in a fisherman’s catch were recorded over one month, and are represented in the following histogram.

Complete the following table.

State whether length of trout is a continuous or discrete variable.
Write down the modal class.
Any trout with length 40 cm or less is returned to the lake.
Calculate the percentage of the fisherman’s catch that is returned to the lake.
The weights in kg, of 80 adult males, were collected and are summarized in the box and whisker plot shown below.
Write down the median weight of the males.
Calculate the interquartile range.
Estimate the number of males who weigh between \(61\) kg and \(66\) kg.
Estimate the mean weight of the lightest \(40\) males.
The IB grades attained by a group of students are listed as follows.
\[{\text{6}}\;\;\;{\text{4}}\;\;\;{\text{5}}\;\;\;{\text{3}}\;\;\;{\text{7}}\;\;\;{\text{3}}\;\;\;{\text{5}}\;\;\;{\text{4}}\;\;\;{\text{2}}\;\;\;{\text{5}}\]
Find the median grade.
Calculate the interquartile range.
Find the probability that a student chosen at random from the group scored at least a grade \(4\).
The weights of 90 students in a school were recorded. The information is displayed in the following table.
Write down the mid interval value for the interval \(50 \leqslant w \leqslant 60\).
Use your graphic display calculator to find an estimate for the mean weight.
Use your graphic display calculator to find an estimate for the standard deviation.
Find the weight that is 3 standard deviations below the mean.
The table below shows the frequency distribution of the number of dental fillings for a group of \(25\) children.
Find the value of \(q\) .
Use your graphic display calculator to find
(i) the mean number of fillings;
(ii) the median number of fillings;
(iii) the standard deviation of the number of fillings.
A group of 20 students travelled to a gymnastics tournament together. Their ages, in years, are given in the following table.

The lower quartile of the ages is 16 and the upper quartile is 18.5.
For the students in this group find the mean age;
For the students in this group write down the median age.
Draw a box-and-whisker diagram, for these students’ ages, on the following grid.

A tetrahedral (four-sided) die has written on it the numbers 1, 2, 3 and 4. The die is rolled many times and the scores are noted. The table below shows the resulting frequency distribution.

The die was rolled a total of 100 times.
The mean score is 2.71.
Write down an equation, in terms of \(x\) and \(y\), for the total number of times the die was rolled.
Using the mean score, write down a second equation in terms of \(x\) and \(y\).
Find the value of \(x\) and of \(y\).
56 students were given a test out of 40 marks. The teacher used the following box and whisker plot to represent the marks of the students.
Write down the median mark.
Write down the 75th percentile mark.
Write down the range of marks.
Estimate the number of students who achieved a mark greater than 32.
A class of 13 Mathematics students received the following grades in their final IB examination.
3 5 3 4 7 3 2 7 5 6 5 3 4
For these grades, find the mode;
For these grades, find the median;
For these grades, find the upper quartile;
For these grades, find the interquartile range.
State which of the following sets of data are discrete.
(i) Speeds of cars travelling along a road.
(ii) Numbers of members in families.
(iii) Maximum daily temperatures.
(iv) Heights of people in a class measured to the nearest cm.
(v) Daily intake of protein by members of a sporting team.
The boxplot below shows the statistics for a set of data.
For this data set write down the value of
(i) the median
(ii) the upper quartile
(iii) the minimum value present
Write down three different integers whose mean is 10.
A survey was carried out on a road to determine the number of passengers in each car (excluding the driver). The table shows the results of the survey.

State whether the data is discrete or continuous.
Write down the mode.
Use your graphic display calculator to find
(i) the mean number of passengers per car;
(ii) the median number of passengers per car;
(iii) the standard deviation.
Toronto’s annual snowfall, x, in cm, has been recorded for the past 176 years. The results are shown in the table.
Write down the modal class.
Write down the mid interval value for the class 6 ≤ x < 10 .
Calculate an estimate of the mean annual snowfall.
Find the number of years for which the annual snowfall was at least 18 cm.
The temperatures in °C, at midday in Geneva, were measured for eight days and the results are recorded below.
7, 4, 5, 4, 8, T, 14, 4
The mean temperature was found to be 7 °C.
Find the value of T.
Write down the mode.
Find the median.
The number of passengers in the first ten carriages of a train is listed below.
6 , 8 , 6 , 3 , 8 , 4 , 8 , 5 , p , p
The mean number of passengers per carriage is 5.6.
Calculate the value of p.
Find the median number of passengers per carriage.
If the passengers in the eleventh carriage are also included, the mean number of passengers per carriage increases to 6.0.
Determine the number of passengers in the eleventh carriage of the train.
The grades obtained by a group of \(20\) IB students are listed below:
Complete the following table for the grades obtained by the students.
Write down the modal grade obtained by the students.
Calculate the median grade obtained by the students.
One student is chosen at random from the group.
Find the probability that this student obtained either grade \(4\) or grade \(5\).
The following histogram shows the weights of a number of frozen chickens in a supermarket. The weights are grouped such that \(1 \leqslant {\text{weight}} < 2\), \(2 \leqslant {\text{weight}} < 3\) and so on.
Find the total number of chickens.
Write down the modal group.
Gabriel chooses a chicken at random.
Find the probability that this chicken weighs less than \(4{\text{ kg}}\).
The cumulative frequency graph shows the heights, in cm, of 80 young trees.
Write down the median height of the trees.
Write down the 75th percentile.
Find the interquartile range.
Estimate the number of trees that are more than 40 cm in height.
A sample of 120 oranges was tested for Vitamin C content. The cumulative frequency curve below represents the Vitamin C content, in milligrams, of these oranges.

The minimum level of Vitamin C content of an orange in the sample was 30.1 milligrams. The maximum level of Vitamin C content of an orange in the sample was 35.0 milligrams.
Giving your answer to one decimal place, write down the value of
(i) the median level of Vitamin C content of the oranges in the sample;
(ii) the lower quartile;
(iii) the upper quartile.
Draw a box-and-whisker diagram on the grid below to represent the Vitamin C content, in milligrams, for this sample.

The length, in cm, of six baseball bats was measured. The lengths are given below.
104.5, 105.1, 104.8, 105.2, 104.9, 104.9
Calculate the exact value of the mean length.
Write your answer to part (a) in the form a × 10k where 1 ≤ a < 10 and \(k \in \mathbb{Z}\).
Marian calculates the mean length and finds it to be 105 cm.
Calculate the percentage error made by Marian.
The table below shows the number of words in the extended essays of an IB class.
Draw a histogram on the grid below for the data in this table.
Write down the modal group.
The maximum word count is \(4000\) words.
Write down the probability that a student chosen at random is on or over the word count.
Consider the frequency histogram for the distribution of the time, \(t\) , in minutes of telephone calls that Helen made last week.
Complete the frequency table for this distribution.
Write down the modal class.
Write down the mid interval value of the \(10 < t \leqslant 15\) class.
Use your graphic display calculator to find an estimate for the mean time.
In an international competition, participants can answer questions in only one of the three following languages: Portuguese, Mandarin or Hindi. 80 participants took part in the competition. The number of participants answering in Portuguese, Mandarin or Hindi is shown in the table.
A boy is chosen at random.
State the number of boys who answered questions in Portuguese.
Find the probability that the boy answered questions in Hindi.
Two girls are selected at random.
Calculate the probability that one girl answered questions in Mandarin and the other answered questions in Hindi.
Write down the following numbers in increasing order.
\(3.5\), \(1.6 \times 10^{−19}\), \(60730\), \(6.073 \times 10^{5}\), \(0.006073 \times 10^6\), \(\pi\), \(9.8 \times 10^{−18}\).
Write down the median of the numbers in part (a).
State which of the numbers in part (a) is irrational.
Complete the following table of values for the height and weight of seven students.
The distribution of the weights, correct to the nearest kilogram, of the members of a football club is shown in the following table.
On the grid below draw a histogram to show the above weight distribution.
Write down the mid-interval value for the \(40 - 49\) interval.
Find an estimate of the mean weight of the members of the club.
Write down an estimate of the standard deviation of their weights.
A random sample of 200 females measured the length of their hair in cm. The results are displayed in the cumulative frequency curve below.
Write down the median length of hair in the sample.
Find the interquartile range for the length of hair in the sample.
Given that the shortest length was \(6{\text{ cm}}\) and the longest \(47{\text{ cm}}\), draw and label a box and whisker plot for the data on the grid provided below.
The cumulative frequency curve shows the percentage marks, given correct to the nearest integer, gained by 500 students in an examination.
The passing grades were determined as given below.
85 to 100 %, grade A
66 to 84 %, grade B
57 to 65 %, grade C
50 to 56 %, grade D
Those scoring less than 50 % failed the examination.
Find the number of students who failed the examination.
Find the number of students who were awarded grade C or better.
The top 20 % of the students are eligible for further study.
Find the lowest mark required to be eligible for further study.
There are \(120\) teachers in a school. Their ages are represented by the cumulative frequency graph below.
Write down the median age.
Find the interquartile range for the ages.
Given that the youngest teacher is \(21\) years old and the oldest is \(72\) years old, represent the information on a box and whisker plot using the scale below.
The diagram below shows the cumulative frequency distribution of the heights in metres of \(600\) trees in a wood.
Write down the median height of the trees.
Calculate the interquartile range of the heights of the trees.
Given that the smallest tree in the wood is \(3{\text{ m}}\) high and the tallest tree is \(28{\text{ m}}\) high, draw the box and whisker plot on the grid below that shows the distribution of trees in the wood.
Consider the following set of data which is plotted on the scatter diagram below.
Write down the coordinates of the mean point \((\bar x{\text{, }}\bar y)\).
Write down the value of \(r\), the Pearson’s product-moment correlation coefficient for this set of data.
Draw the regression line for \(y\) on \(x\) on the set of axes above.
A group of students were asked how long they spend practising mathematics during the week. The results are shown in the following table.
It is known that \(35 < a < 52\) .
Write down
i) the modal class;
ii) the mid-interval value of the modal class;
iii) the class in which the median lies.
For this group of students, the estimated mean number of hours spent practising mathematics is \(2.69\).
Calculate the value of \(a\) .
The cumulative frequency graph shows the amount of time in minutes, 200 students spend waiting for their train on a particular morning.
Write down the median waiting time.
Find the interquartile range for the waiting time.
Draw a box and whisker plot on the grid below to represent this information.
Two groups of 40 students were asked how many books they have read in the last two months. The results for the first group are shown in the following table.

The quartiles for these results are 3 and 5.
Write down the value of the median for these results.
Draw a box-and-whisker diagram for these results on the following grid.

The results for the second group of 40 students are shown in the following box-and-whisker diagram.

Estimate the number of students in the second group who have read at least 6 books.
120 Mathematics students in a school sat an examination. Their scores (given as a percentage) were summarized on a cumulative frequency diagram. This diagram is given below.
Complete the grouped frequency table for the students.
Write down the mid-interval value of the \(40 < x \leqslant 60\) interval.
Calculate an estimate of the mean examination score of the students.
In a high school, 160 students completed a questionnaire which asked for the number of people they are following on a social media website. The results were recorded in the following box-and-whisker diagram.
The following incomplete table shows the distribution of the responses from these 160 students.
Write down the median.
Complete the table.
Write down the mid-interval value for the 100 < x ≤ 150 group.
Using the table, calculate an estimate for the mean number of people being followed on the social media website by these 160 students.
A cumulative frequency graph is given below which shows the height of students in a school.
Write down the median height of the students.
Write down the 25th percentile.
Write down the 75th percentile.
The height of the tallest student is 195 cm and the height of the shortest student is 136 cm.
Draw a box and whisker plot on the grid below to represent the heights of the students in the school.
The histogram shows the time, t, in minutes, that it takes the customers of a restaurant to eat their lunch on one particular day. Each customer took less than 25 minutes.
The histogram is incomplete, and only shows data for 0 ≤ t < 20.
The mean time it took all customers to eat their lunch was estimated to be 12 minutes.
It was found that k customers took between 20 and 25 minutes to eat their lunch.
Write down the mid-interval value for 10 ≤ t < 15.
Write down the total number of customers in terms of k.
Calculate the value of k.
Hence, complete the histogram.
The table shows the number of bicycles owned by 50 households.
Write down the value of
(i) t ;
(ii) w .
Indicate with a tick () whether the following statements are True or False.
In a school 160 students sat a mathematics examination. Their scores, given as marks out of 90, are summarized on the cumulative frequency diagram.
Write down the median score.
The lower quartile of these scores is 40.
Find the interquartile range.
The lowest score was 6 marks and the highest score was 90 marks.
Draw a box-and-whisker diagram on the grid below to represent the students’ examination scores.